Computer Engineering / Computer Science 126

Dr. Jim Keller, Dr. Michael Jurczyk, and Jerry Moore
[Chapter 1] [Chapter 2] [Chapter 3] [Chapter 4]

The traditional number system that we all know and use everyday is called a positional number system. In this system, a number is represented by a string of digits where each digit position has an associated weight. The value of the number is the weighted sum of the digits, for example:

6437.92 = 6 × 1000 + 4 × 100 + 3 × 10 + 7 × 1 + 9 × ¹/₁₀ + 2 × ¹/₁₀₀

Here it is clear to see that the 6, 4, 3, 7, 9, and 2 are the digits that are multiplied by weights that are powers of ten. By rewriting this, we can see the pattern more clearly:

6437.92 = 6 × 10³ + 4 × 10² + 3 × 10¹ + 7 × 10⁰ + 9 × 10^-1 + 2 × 10^-2

For the above example, 10 is called the base or radix of the number system. We are normally used to dealing with mathematics in base 10, although the radix can be any integer r ³ 2. In general, a number can be written: d_p-1 d_p-2 × × × d₁ d₀ . d_-1 d_-2 × × × d_-n

where d_i is the digit in position i which is a non-negative integer less than the base, p is the number of digits to the left of the decimal point, and n is the number of digits to the right of the decimal point. The true name of the point is the radix point; it is only called the decimal point when we’re actually dealing with base 10 number systems. If the radix point is missing, it is assumed to be to the right of the rightmost digit. The actual value D of this general number can be found by the following formula:

Except for possible leading and trailing zeroes, the representation of a number in a positional number system is unique. (Obviously, 0397.2400 is the same as 397.24 and so on.) The leftmost digit of a number is called the most significant digit (MSD); the rightmost digit is called the least significant digit (LSD).

For digital systems, we will use the base 2 (or binary) number system, because we are representing digital signals that can be in only two possible states: low or high, off or on, etc. The signals in these circuits are represented by binary digits (or bits) that have one of two values, 0 and 1, corresponding to the "off" and "on" state respectively. Thus, the binary radix is normally used to represent number in a digital system. The general form of a binary number is:

b_p-1 b_p-2 × × × b₁ b₀ . b_-1 b_-2 × × × b_-n

and its value is:

In a binary number, the radix point is called the binary point. The base or radix that the number is represented in is indicated by the subscript on the number. Some examples of binary numbers and their decimal equivalents are listed below:

11010₂ = 1 × 2⁴ +1 × 2³ + 0 × 2² + 1 × 2¹ + 0 × 2⁰ = 26₁₀

110₂ = 1 × 2² + 1 × 2¹ + 0 × 2⁰ = 6₁₀

10101.01₂ = 1 × 2⁴ + 0 × 2³ + 1 × 2² + 0 × 2¹ + 1 × 2⁰ + 0 × 2^-1 + 1 × 2^-2 = 21.25₁₀

The leftmost bit of a binary number is called the most significant bit (MSB); the rightmost is the least significant bit (LSB).

We use radix 10 in our everyday calculations, while a computer does its operations in radix 2. These bases are the most important but are not the only ones that are useful. The octal number system uses radix 8, and is represented by digits which can range from 0 - 7 (these correspond to all 3-bit binary representations.) The hexadecimal number system uses radix 16 and is represented by digits 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F (see Table 1). The hexadecimal digits correspond to all 4-bit binary representations. Remember that when a number system is in radix N, it needs N digits (or symbols) to represent the range [0 - (N-1)].

Table 1 - Binary, decimal, octal, and hexadecimal numbers

Computers can work with the octal and hexadecimal number systems are easier because their bases are powers of 2. Each 3-bit string can be uniquely represented by one octal digit, while each 4-bit string can be uniquely represented by one hexadecimal digit. To convert a binary number to octal, start at the binary point (the decimal point) and work left while separating bits into groups of three. If you need to, append leading zeroes to the MSB of the binary number to complete the last group (since this does not change the value of the number.) If a binary number contains digits to the right of the binary point, we can convert them as well by starting at the binary point and working right while separating them into groups of three. Once all bits are grouped, then replace the groups with the proper octal digit:

1010111011₂ = 001 010 111 011₂ = 1273₈

101110.0101₂ = 101 110. 010 100₂ = 56.24₈

The procedure for converting binary to hexadecimal is similar, except we use groups of four bits:

10111111001₂ = 0101 1111 1001₂ = 5F9₁₆

11011011.000100001₂ = 1101 1011. 0001 0000 1000₂ = DB.108₁₆

Remember that we add leading zeros if we need them to fill out the groups of three or four.

To convert from octal or hexadecimal back to binary is just a matter of replacing each octal or hexadecimal digit with the corresponding 3- or 4-bit string, as shown below:

1672₈ = 001 110 111 010₂

2571.63₈ = 010 101 111 001. 110 011₂

CD97₁₆ = 1100 1101 1001 0111₂

F39A.8B₁₆ = 1111 0011 1001 1010. 1000 1011₂

A byte is defined to be a group of 8 bits. Sometimes a group of four bits is referred to as a nibble. Words are larger groups of bits; common values are 16, 32, and 64-bit words. Hexadecimal numbers neatly break down into one byte, or two nibbles, while octal numbers do not. As a result, the hexadecimal number system has recently become more popular in computers and programming.

Where conversion between two radices that are powers of 2 can be done using simple substitution, this is not the case when converting to other bases. In this section, we show how to convert a number in radix 2, 8, or 16 to radix 10 and vice versa, using radix 10 arithmetic. Remember that the value of a number in any radix is given by the formula:

where D is the value, r is the radix of the number, d_i is the digit in position i, and there are p digits to the left of the radix point and n to the right. Thus, the value of the number can be found by converting each digit of the number to its radix-10 equivalent and expanding the formula using radix-10 arithmetic. Some examples are:

9C₁₆ = 9 × 16¹ + C × 16⁰ = 156₁₀

E4.C₁₆ = 14 × 16¹ + 4 × 16⁰ + 12 × 16^-1 = 228.75₁₀

713.2₈ = 7 × 8² + 1 × 8¹ + 3 × 8⁰ + 2 × 8^-1 = 459.25₁₀

If we multiply out the above formula, we get a shortcut for converting numbers to base 10 as follows:

This formula forms a basis for a very convenient method of converting a decimal number D to a radix r. Consider what happens if we divide the formula by r. Since the parenthesized part of the formula is evenly divisible by r, the quotient Q and remainder R are:

Thus d₀ can be computed as the remainder of the long division of D by r. Furthermore, the quotient Q has the same form as the original formula. Therefore, successive divisions by r will yield successive digits of D from right to left, until all the digits of D have been derived. Examples are below:

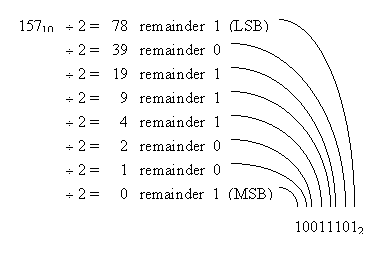
Conversion from one base to another is sometimes easier as a two step process.

Table 2 summarizes methods for converting among the common radices.

Table 2 - Conversion Methods for Common Radices

Addition and subtraction of nondecimal numbers is very similar to decimal numbers, except we are using different bases. To add two binary numbers, we start from the right and work left, adding each column and including the carry out of each column in the next column’s sum. In the first example below (on the left), you begin by adding the two 1’s together, writing the remainder in the same column, and writing the carry above the next column. This works the same for binary number containing binary points. Carries on either side of the binary point are treated the same. Remember that these are simple examples. The carry can be any positive number.

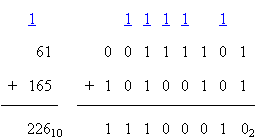
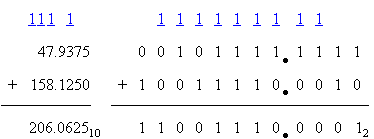
In the two examples above, the blue (or underlined) 1’s indicate the carry of 1.

Binary subtraction is performed similarly, using borrows instead of carries between steps. (See the two examples below.) Notice in the first example (on the left) that the first two columns are subtracted normally. Then the top number of the third column requires a borrow from the fourth column, but the fourth column has nothing to "lend" so it looks to the fifth column for a borrow. The fifth column donates its one, leaving its value at zero. The fourth column receives the borrow from the fifth, which is equivalent to adding the base to the top number, making it a binary two. Then the third column can finally borrow from the fourth column.

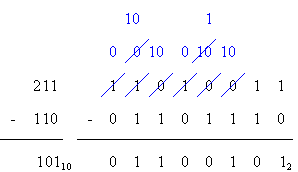
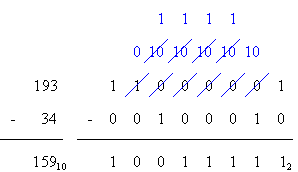
The base is added to the third column, while one (the borrow) is subtracted from the fourth column. Now the subtraction can continue normally until the next borrow is needed.

Multiplication and division in a radix system other than base 10 is performed in exactly the same manner as is base 10. The only difference is that you have to "think" in the different radix system. For example:

Note that while the decimal division terminates, neither the binary nor the hexadecimal does. This points out that conversions between number systems may not be exact (leading to errors in calculations). The problem arises out of the fact that computer systems have a limited number of bits to represent numbers.

Suppose that a computer system has 8 bits (one byte) to represent integers. Then each bit can hold either a 0 or 1, and so, there are possible "codes" to represent the numbers. Hence, the range of values for the numbers is . (If there are m bits, then there are codes available). The method of representing the non negative integers is just to convert from decimal to binary. This is called the Binary Value Code (BVC). When adding two fixed length BVC integers, the sum can get too big to fit into the amount of storage available. For example, when adding 1 to 255, the answer is 256 in decimal, but if only 8 bits are available, then we have a problem in binary. In fact,

255 1 1 1 1 1 1 1 1

+ 1 0 0 0 0 0 0 0 1

256 1÷ 0 0 0 0 0 0 0 0

The 1 in the "9th" bit position is called the carry bit (all ALU’s record this bit). The answer (in 8 bits) is ZERO, clearly wrong. This is called overflow for BVC numbers (when the answer doesn’t fit into the fixed length). Overflow for BVC numbers also happens when you try to subtract a larger number from a smaller one - you need to "borrow" into the most significant bit. This is because the "answer" is not correct since there is no way in BVC to encode negative numbers (the answer in this case should be negative).

What if we want to encode negative numbers also? We must define a code for negative integers that is capable of being used for subtraction in a straight forward way. First, we must note that to include negative numbers, we effectively half the maximum range of the positive values (we need half of the codes for the negative numbers). So, 8-bit positive and negative numbers must end up in the range:

-128, -127, ..., -1, 0, 1, ..., 127 or .

Note that this range is not balanced because 0 is considered a "positive" representation, i.e., there is one more negative number than positive number.

The simplest method is to use "sign-magnitude", i.e., represent the magnitude of the number in 7 bits (or m-1 bits for an m-bit representation), and reserve the 8th bit (or the mth bit) for the sign. Thus, 52 would be represented as 0110100, while -52 is represented by 10110100. This seems easy. But there are problems. Should 0 have a negative? (10000000) There is the problem with the non balanced number line (we lose -128, because we can’t represent +128 in 7 bits). Also, addition and subtraction get complicated because we always need to check signs and perform different operations based on the signs of the numbers. If we just try to add directly, we run into problems, i.e.,

- 1 Þ 1 0 0 0 0 0 0 1

+1 Þ 0 0 0 0 0 0 0 1

0 1 0 0 0 0 0 1 0

We ask the question: What 8-bit code, when added to +1 (0000 0001) will give 0? Consider the 8-bit binary number 1111 1111. When we add, we get all zero’s in the low eight bits (see addition above). Is there a way to have 1111 1111 represent -1? The two’s complement format provides that mechanism. Formally, the 2’s complement of an n-bit binary number, x, is defined as . So, for 8-bit numbers,

1 0000 0000

- 0000 0001

1111 1111

Note that up to n-bits. To create the 2’s complement of a number in the range , we can subtract from (the hard way to do it) or we can use the 1’s complement (which just reverses the bits), and then add 1. For example, recall that 26₁₀ = 0001 1010 as an 8-bit binary number. Then -26 would be:

1| 0000 0000

- 0001 1010

1110 0110

or taking the 1’s complement and adding 1 we get 1110 0101

+0000 0001

1110 0110

Note that the most significant bit of the negative number is actually a 1, while the msb of a positive value is always a 0. To check this, add any number and it’s 2’s complement, e.g.,

0001 1010

0000 0000

Note that there is a carry out, but to within 8-bits, the sum is zero.

A fast "trick" to compute the 2’s complement is to start at the right, keeping all bits up to and including the first 1, then "flip" the remaining bits. An interesting issue arises with -128, since there is no +128. It turns out that -128 is 1000 0000 in 2’s complement format, but it is its own 2’s complement (kinda weird, but ...). Of course, zero is also its own 2’s complement.

Hence, within the 2’s complement format, there are positive and negative integers (and zero) and addition is as before (just add bits). Subtraction now becomes "adding the negative", i.e., take the 2’s complement of the subtrahend and add it to the minuend. Work out some examples to convince yourself that this is correct. Now, in this format, overflow is defined differently. Adding a positive and a negative number in the range will always produce a number in that range, and thus will NOT cause overflow (even if there is a carry out). Adding 2 positive numbers or 2 negative numbers could result in an overflow if the answer has the wrong sign (i.e., if the sum of two positives is negative: msb = 1; or the sum of two negatives is positive: msb = 0). This condition is checked and "flagged" by the hardware in the ALU of the microprocessor. However, you have to decide what to do with the information. Check the examples in class and the homework to understand the overflow concept.

There are many types of codes that are used in computer systems. Two that we will consider are Binary Coded Decimal (BCD) and ASCII codes for alphanumeric characters. BCD codes are 4-bit binary codes for the decimal digits (0 - 9). These codes are just the Hexadecimal representations of the 10 decimal digits (0000 - 1001). They are used to represent strings of decimal digits used for accounting-type purposes, display of digits (like on watches), etc. Thus, 12:00 would be represented as 0001 0010: 0000 0000. Note that certain 4-bit codes are illegal for BCD representation, e.g., 1010 has no BCD meaning. This makes it somewhat difficult to do arithmetic in BCD (can’t just add in binary). Many processors, including the M68HC11, support special instructions to aid in such BCD arithmetic (the "DAA" instruction in the M68HC11 handles the carry for BCD digits).

Alphanumeric characters must have a means of representation also. The most common code for characters is called the ASCII code (American Standard Code for Information Interchange). It uses 7-bits to represent characters. Thus, it accommodates 128 characters which include upper and lower case letters, the digits, punctuation marks, and special characters (like carriage return, escape, etc.). Normally, the code is stuck into a byte for ease of display. For example, CECS 126 would be coded in Hex as 43 45 43 53 20 31 32 35. Note that the "blank" or space also has a code, "20". The DEL key is coded as "7F" (the largest code possible in ASCII). These codes are used in transmitting information to and from the processor and peripheral devices, like the keyboard and monitor, as well as for storing text information internally.