|
A Fast Numerical Solution
for General Robotic Manipulators Using Parallel Processing
by
Siavash Farzan
Introduction
A general robotic manipulator is
a combination of links and joints, where the joints are either
prismatic (P) or revolute(R). In order to move the robotic end-effector
along a certain path, the joint variables 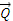 (t)
must be controlled until the end-effector reaches the desired
position and orientation (i.e. pose (t)
must be controlled until the end-effector reaches the desired
position and orientation (i.e. pose 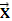 (t),
where (t),
where 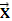 (t) = f( (t) = f(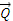 (t))
). Hence, given a desired pose (t))
). Hence, given a desired pose 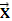 (t),
it is necessary to solve the inverse kinematics equation (t),
it is necessary to solve the inverse kinematics equation 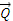 (t)
= f-1( (t)
= f-1(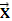 (t)). (t)).
Here, we propose a robust and
fast solution for the inverse kinematical problem of general
serial manipulators – i.e. any number and any combination of
revolute and prismatic joints. The algorithm only requires the
Denavit-Hartenberg (D-H) representation of the robot as input
and no training or robot dependent optimization function is
needed. In order to handle singularities and to overcome the
possibility of multiple paths in redundant robots, our approach
relies on the computation of multiple (parallel) numerical
estimations of the inverse Jacobian while it selects the current
best path to the desire configuration of the end-effector. But
unlike other iterative methods, our method achieves
sub-millimeter accuracy in average of 20.48ms. The algorithm was
implemented in C/C++ using 16 POSIX threads, and it can be
easily expanded to use more threads and/or multi-core GPUs. We
demonstrate the high accuracy and the real-time performance of our
method by testing it with five different robots, at both
non-singular and singular configurations, including a 7-DoF
redundant robot.
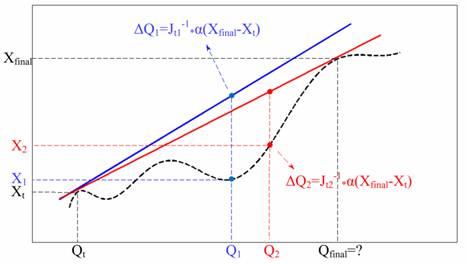
Figure 1. Visual representation of
the proposed method in one dimension
Related work
From Computational Intelligence to
Robotics: Using Evolutionary Algorithms to Solve the Inverse
Kinematics Problem
by
Siavash Farzan
Introduction
Computational Intelligence has always had an impact on
different areas including Robotics and Automation. In this project a robust and
fast evolutionary-like solution for the inverse kinematic problem of general
serial manipulators – i.e. any number and any combination of revolute and
prismatic joints is proposed. It uses an iterative numerical approximation of
the Inverse Jacobian and unlike other iterative methods, it is accurate and fast
and works for any generic robotic manipulator –redundant or not- even at
singular configuration of the joint variables.
This approach is
compared with some other evolutionary algorithms based on
Genetic Algorithm to find the strengths and weaknesses of
different CI methods for this problem.
We demonstrate
that high accuracy and the real time performance of our method
by comparing it with two different approaches proposed in other
papers, including a GPU-based one.
Experimental
results carried out on different robots showed that the new
proposed approach is able to find a better solution compared to
genetic algorithm methods; with fewer iterations, sub-millimeter
accuracy and in real time.
The algorithm
was implemented in C/C++ using 16 POSIX threads, and it can be
easily expanded to use more threads and/or many-core GPUs.
Third place poster award, 6th annual MU IEEE
Computational Intelligence Society (CIS) poster contest
References
- S. Farzan and G. N. DeSouza, "From D-H to Inverse
Kinematics: A Fast Numerical Solution for General Robotic
Manipulators Using Parallel Processing", Intelligent Robots
and Systems (IROS), 2013 IEEE International Conference.
(Submitted)
|